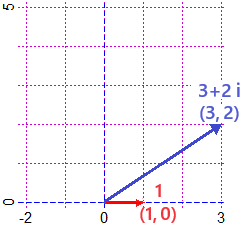
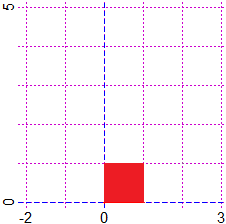
I vettori possono essere rappresentati anche come numeri complessi. Ad esempio il vettore (3,2) può essere rappresentato col numero complesso 3+2 i dove 3 è l'ascissa e 2 è l'ordinata. Il vettore (1,0) è invece rappresentabile con 1+0 i, scritto più semplicemente come 1.  Se hai studiato i numeri complessi capirai facilmente la seguente animazione, che illustra come i punti del quadrato illustrato a destra sono trasformati pensandoli come numeri complessi e moltiplicandoli per il numero complesso 3+2 i.

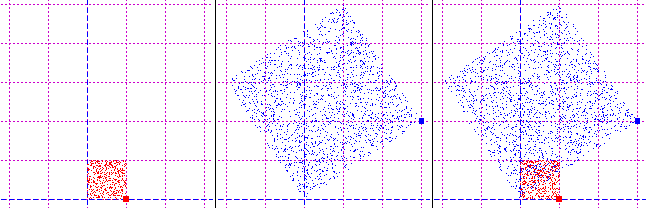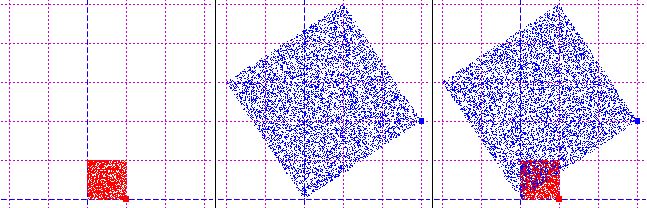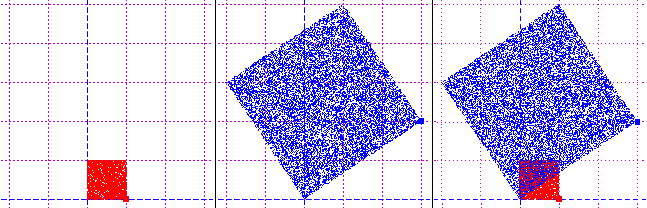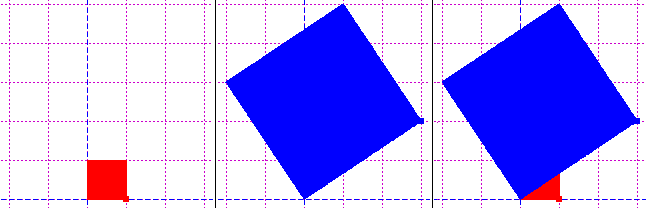
Il punto (0,0) rimane immutato, il punto (1,0) viene trasformato in (3,2) ovvero il vettore (0,0)-(1,0) viene allungato e ruotato fino a coincidere col vettore (0,0)-(3,2), come si vedeva nella figura iniziale.
Analogamente vengono trasformati gli altri punti:  il punto (0,1) fa a finire in (-2,3),  il punto (1,1) va a finire in (1,5).  Tutto il quadrato rosso viene ingrandito e ruotato fino a trasformarsi nel quadrato blu.

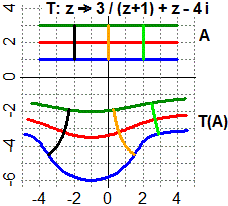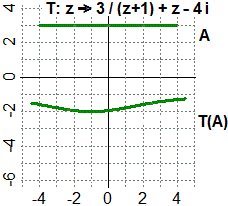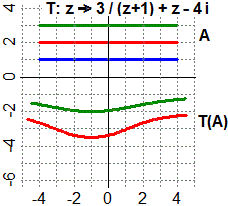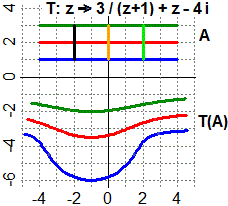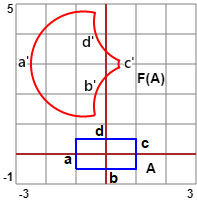Si possono estendere ai numeri complessi molte delle operazioni e della funzioni tra numeri reali. I numeri complessi hanno numerose applicazioni, che potrai esaminare se proseguirai gli studi in ambito scientifico. Accenniamo solo ad una generalizzazione dell'esempio precedente:  le trasformazioni che associano a  z = x+y i  un termine ottenuto componendo le quattro operazioni trasformano linee tra loro prependicolari in linee che sono ancora tali.  A sinistra un esempio animato.  A destra alcune trasformazioni operate dalla funzione F: z → z / (1.4 + z) + 3 i.